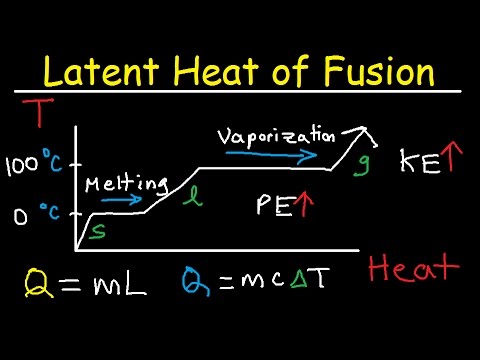
Latent heat of fusion is a fundamental concept in thermodynamics and physics, describing the energy required to change a substance from solid to liquid (melting) or from liquid to solid (freezing) without a temperature change.
Table of Contents
What is the Latent Heat of Fusion?
The latent heat of fusion refers to the heat energy needed to convert a solid to a liquid at a constant temperature. Unlike heat used to raise temperature, latent heat only changes the state of the substance without affecting its temperature.
Key Concept
When heat is applied to a substance at its melting point, the energy goes into breaking molecular bonds rather than increasing temperature. This explains why ice melts at 0°C but does not immediately warm up until it is completely liqui
Latent Heat of Fusion Formula
The formula to calculate the heat energy required for melting or freezing a substance is-
Q = m × L
Where-
- Q = Heat energy absorbed or released (in Joules, J)
- m = Mass of the substance (in kilograms, kg)
- L = Latent heat of fusion (in Joules per kilogram, J/kg)
This equation applies only during a phase change when a solid turns into a liquid or vice versa, while the temperature remains constant.
Example Calculation- Melting Ice
Problem- How much heat is required to melt 2 kg of ice at 0°C?
Given Data-
- Mass of ice (m) = 2 kg
- Latent heat of fusion of ice (L) = 334,000 J/kg
Calculation-
Q = m × L
Q = 2 × 334,000
Q = 668,000 J
Final Answer- 668,000 Joules of heat energy is required to completely melt 2 kg of ice at 0°C.
Key Takeaway-
- The temperature of ice remains constant at 0°C while melting because all the energy is used to break molecular bonds instead of increasing temperature.
What If the Substance Heats Up Instead of Melting?
If a substance only changes temperature (without changing state), we use-
Q = mcΔt
Where-
- Q = Heat energy absorbed or released (J)
- m = Mass of the substance (kg)
- c = Specific heat capacity (J/kg°C)
- Δt = Temperature change (Final temp – Initial temp)
Example Calculation- Heating Water
Problem- How much heat is needed to raise the temperature of 2 kg of water from 0°C to 50°C?
Given Data-
- Mass of water (m) = 2 kg
- Specific heat capacity of water (c) = 4186 J/kg°C
- Temperature change (Δt) = 50°C – 0°C = 50°C
Calculation-
Q = mcΔt
Q = 2 × 4186 × 50
Q = 418,600 J
Final Answer- 418,600 Joules of heat energy is needed to raise the temperature of 2 kg of water from 0°C to 50°C.
What If Both Melting and Heating Happen?
When a substance first melts and then heats up, we combine both formulas-
Q = mL + mcΔt
This equation consists of two parts-
- mL – Heat energy required to melt the substance
- mcΔt – Heat energy required to raise or lower the temperature
Example Calculation- Melting Ice and Heating Water
We want to calculate the total heat energy needed to-
- Melt 2 kg of ice at 0°C into water
- Heat the water from 0°C to 50°C
Step 1- Melting the Ice
Q₁ = m × L
Q₁ = 2 × 334,000
Q₁ = 668,000 J
Step 2- Heating the Water
Q₂ = mcΔt
Q₂ = 2 × 4186 × 50
Q₂ = 418,600 J
Total Heat Energy Required
Q = Q₁ + Q₂
Q = 668,000 + 418,600
Q = 1,086,600 J (or 1.086 MJ)
Final Answer- 1.086 MJ of heat energy is required to melt 2 kg of ice at 0°C and heat the resulting water to 50°C.
Comparison of Heat Energy Formulas
| Formula | When to Use It | Example |
| Q = mL | Used for phase changes (melting or freezing) at constant temperature. | Melting ice into water at 0°C |
| Q = mcΔt | Used when a substance is changing temperature without a phase change. | Heating water from 0°C to 50°C |
| Q = mL + mcΔt | Used when a substance undergoes both phase change and temperature change. | Melting ice and then heating water |
Key Takeaways
✔ Use Q = mL when a substance is melting or freezing.
✔ Use Q = mcΔt when a substance is heating up or cooling down.
✔ Use Q = mL + mcΔt when both phase change and temperature change happen.
✔ Temperature remains constant during a phase change because the heat energy is used to break or form molecular bonds instead of increasing temperature.These principles are essential in physics, engineering and thermodynamics for understanding heat transfer and phase changes.
